Sometime in 1974 while I was in 6th form (now called year 12) at Karingal High School in Frankston (40km from Melbourne), fellow student Bradley McDonald wrote the following nonsense integral in the front page of my maths book in blue fountain pen.

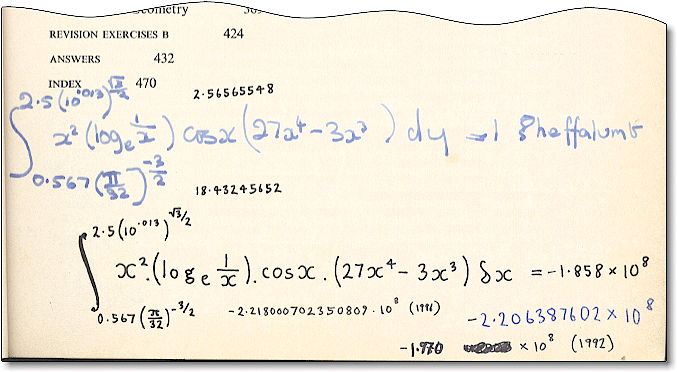
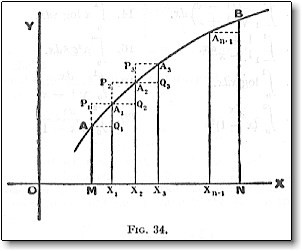
Later that day I neatly rewrote the integral underneath Brad's scrawl using my black pen. I assumed that the dy in Brad's integral was an accident and I changed it to dx to make the integral meaningful. So began the search for the value of one delta heffalumb (or is it a sigma heffalumb?). In 1974 I didn't have the skill to explicitly deconstruct the integral, nor did I have a programmable calculator, so I've got no idea now how I came to write a value for the integral of -1.858x10⁸. I can only guess now that I might have written a Minitran (miniature Fortran) program that my maths teacher ran for me at Monash University . No record exists of the program and my memory of learning to program in High School is vague now. If I did write a Minitran program, then I assume I would have approximated the integral value by summing trapezoidal slices as illustrated in the following picture.

Although my 1974 value of -1.858x10⁸ is about 16% short of the actual value, it's surprisingly close and in the right order of magnitude. The real value would be revealed decades later.

I don't know if it was luck or instinct, but Brad's random integral is continuous in the ranges he specified. The integral limits turn out to be approximately:

upper limit = 2.56566
lower limit = 18.4325

If we define the function under the integral in Mathematica and simply plot it between the limits we see that it seems to oscillate and grow rapidly, obviously due to the cosine and polynomial terms. Luckily the log term only contributes a small negative range in the interval. Here we define the function and the limits as real numbers and plot the behaviour.

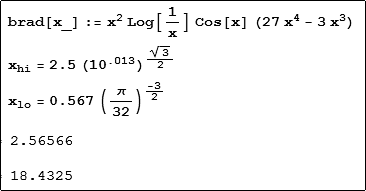
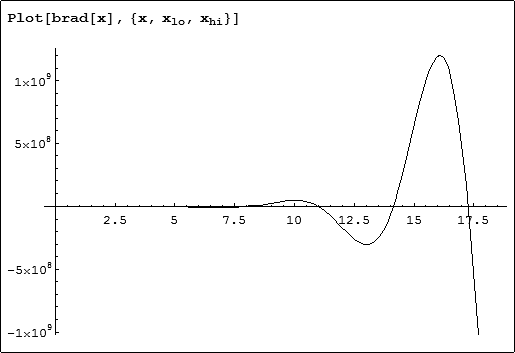
The function oscillates due to the cosine term and it increases rapidly due to the polynomial terms. The plot at this scale can't reveal the oscillations on the left side. A logarithmic flattened version of the plot shows the shape of the function.

Sharp EL-5120 Calculator

After the 1974 vintage value of -1.858x10⁸ the problem was forgotten for 17 years. In 1991 I purchased a Sharp EL-5030 programmable calculator with 1K of memory and used it to evaluate the integral by the method of summing trapezoidal slices. I found that the width of the slices caused the value to vary considerably with a mean value that seemed to converge around -1.97x10⁸, so that was the best I could do in 1991. The EL-5030 performed wonderfully and lasted until late 2000 when it developed a fault in the internal contacts and sadly it had to be discarded.

In early 2002 I purchased a Sharp EL-5120 which has 1211 bytes of user memory and can be programmed with a simplified BASIC style language (image right). I must wonder why after 10 years that the new EL-5120 Sharp calculator has that same amount of memory as the old EL-5030. Surely, in the 21st century we should be measuring the memory in pocket calculators in megabytes, not kilobytes. The EL-5120 has a built-in Solver Function which can evaluate Integrals using Simpson's Rule with a selectable number of increments. In July 2002 I turned the EL-5120 lose in Bradley's Integral and was amazed to find that the first 6 digits of the correct value popped-out. The following table shows the results using different increment counts. The default is 100.

Increments	Solver Value
50	-2.2181315x108
100	-2.2180088x108
200	-2.2180012x108
300	-2.2180009x108

Sadly again, in early March 2012 the EL-5120 developed a fault in the display pixels which made some characters render incompletely, so for example an 8 would look like a 3 in certain positions. I placed the calculator back in its original package with the manual and now it's archived in the bookshelf as a historical curiosity. I intended to order the Sharp EL-W506 as a replacement, but accidentally purchased the EL-506W which is the standard version without the realistic "WriteView" display. I was tricked by the anagram of the names when I filled-in the web order form. I had already discarded the packaging, so an exchange is not likely. Perhaps I will go a step further and get the EL-W531G which is programmable and has the "WriteView" display. I have wasted $40 + $10 postage on a brand new EL-506W which I don't like. For more information see: Calculators

In 1996 I used Mathematica for Students version 2.2 to evaluate the Integral as follows.

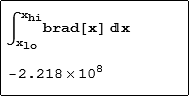
So, 22 years later the true answer is revealed. I trusted the value was correct, but I wondered why there was so little precision and didn't take the time to investigate further.

Four years later, in early 2000 I acquired a copy of Mathematica version 4.0 and my knowledge of how to use it had improved somewhat, especially in regard to issues of numerical precision. Now I redefine the integral limits to be exact values and show them with increased precision. Notice how Mathematica has cleverly simplified the form of the limits.

Now we are ready to re-evaluate the integral with exact values, avoiding machine precision values. Finally I print the value as a plain number with 30 digits of precision.

Are you prepared for the stunning result that follows?!

This seems utterly incredible, but Mathematica has evaluated this integral explicitly using mostly elementary functions, familiar constants, roots and powers. I say mostly elementary because the SinIntegral and CosIntegral functions have slipped into the result (follow the links to Mathworld to learn more about those functions). Finally, here is the value of Bradley's Integral to 30 digits of accuracy:

Year	Value	Error	Method
1974	-1.858 x 108	28%	Unknown, possibly a Minitran program using trapezoidal sums.
1991	-1.97 x 108	11%	Sharp EL-5030 calculator using trapezoidal sums.
1996	-2.218 x 108	0.00003%	Mathematica 2.2 using machine precision numbers.
2002	-2.21800090 x 108	0.000009%	Sharp EL-5120 calculator's built-in Simpson's Rule solver.
2002	exact value	0%	Mathematica 4 using arbitrary precision.

Zip of the Mathematica 4 Notebook for calculations on this page.