School Days
In the latter years of high school we were progressively introduced to subjects like elementary probability and statistics,
permutations and combinations,
the Normal and Poisson
distributions, correlation, expectation, and so on.
Quite often during these years, the expression random number was used, but the subject of random numbers was never the formal part of any course
and the exact meaning of random number remained tantalisingly unclear. I had this comical image in my head of hundreds of monkeys throwing dice
or hammering away at typewriters to create randomness
(that wouldn't work of course! See this Simpsons episode clip).
The topic of random numbers or randomness in general was not discussed in any publications I had access to, so the whole subject remained idle for many years.
I was bemused to find a list of random numbers on page 38 of my Four-Figure Mathematical Tables book.
If you look closely you'll see that the numbers are familar. You're looking at the decimal part of π. Firstly, it's really lazy
of the authors to simply stick π digits into a table and claim they're random. Secondly, this opens up a random can of worms,
because it is suspected that the decimal digits of π are actually random, but this remains unproven. For a technical discussion
of this, see Wikipedia's article on Normal Number and for a more casual
discussion see Math is Fun.
Jumping into the future of 1986 for a moment, it's when I purchased a copy of the famous
Handbook of Mathematical Functions by
Abramowitz and Stegun, originally published in 1964. I never knew about this book in high school, and had I seen one back then I would have thought it
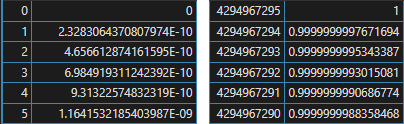
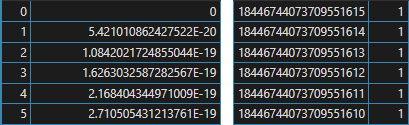
was a set of log tables that fell through a wormhole from the distant future. I was bemused once again to see 2500 five-digit random numbers occupying
pages 991 to 995. A footnote says:
Compiled from Rand Corporation. A million random digits with 100,000 normal deviates. The Free Press, Glencoe, Ill., 1955 (with permission).
Programming
In 1974 I was lucky enough to be able to use a Monash University Minitran computer to learn to write my first computer programs
(see my Computers History page for more details). I was fascinated by the function F4 which
generated random numbers, so I used it to print random bars and points made from asterisks. Therefore the first hobby program I ever
wrote plotted random numbers. Sadly, I don't have any copies of the 15×11 inch fanfold paper printouts from the time.
In 1992, the very first C program I wrote with Microsoft C/C++ 7 under DOS 5.0 generated random coloured pixels on the screen.
A few months later, the first Windows program I wrote with the Microsoft SDK 3.1 filled the window client area with random lines.
My first Windows screen saver filled the screen with customisable random shapes and colours.
The first Java applet I wrote in early 1996 mimicked the workings of my screen saver in miniature.
It seems that every "hello world" program I have written in the last 30 years when learning a new programming language seems to play with random numbers.
Until late 2021 I had some Silverlight applications called Boxes, Hypno
and SilverRand which used random numbers to generate entertaining visual effects.
Sadly, Silverlight was deprecated and all that remains on those web pages are screenshots of the original animations.
%20-%20A01%20-%20Front%20Cover.jpg)












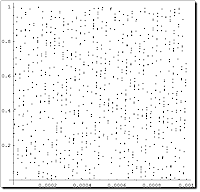
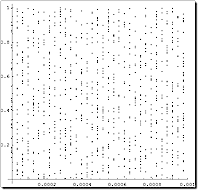
 Notebook
Notebook