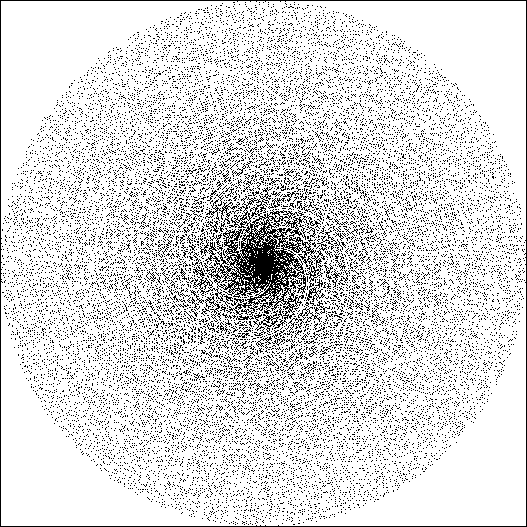
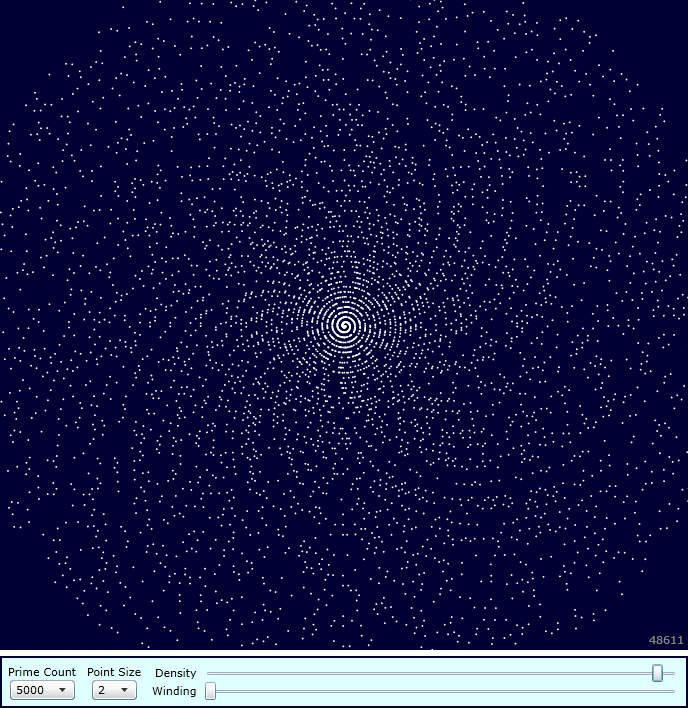
Prime numbers plotted on a spiral number line, inspired by the square spiral of Stanlislaw Ulam (see:The Ulam spiral phenomenon). In my plot I'm not using a "square spiral" like Ulam, I'm using a real spiral where you can imagine the number-line is wound into a smooth spiral and each prime on the wound line is marked with a dot. As the winding and density variables are adjusted in the Mathematica program the "tightness" of the winding and the "stretching" of the line show mysterious patterns of primes and composites.

This small sample shows the spiral with very low winding and density to reveal its real shape. Primes can be seen dotted along the wound number-line. In the main image below the winding is much tighter and the density of the line is much higher.

Off[General::Spell1];
winding = 20000; (* Higher values for tighter winding *)
density = 150; (* Higher values to "pack" the primes closer together *)
count = 45000; (* How many points to plot *)
genpoint[n_Integer] := {(n Sin[Prime[n]/density])/winding,(n Cos[Prime[n]/density])/winding};
rad = genpoint[count];
mrad = Max[1,Sqrt[rad[[1]]^2+rad[[2]]^2]];
(*N[{rad,mrad}]*)
points = Table[genpoint[n],{n,1,count}];
ListPlot[points,
  PlotStyle->{AbsolutePointSize[0.01]},
  AspectRatio->Automatic,
  Frame->True,GridLines->None,
  Axes->None,FrameTicks->None,
  PlotRange->{{-1 mrad,mrad},{-1 mrad,mrad}}];];

Thanks to Chris who contacted me in Jun 2008 to say he had converted the spiral code into a Mathematica 6.0.1 Interactive Notebook and submitted it for publication on the Wolfram Demonstrations web site: http://demonstrations.wolfram.com/TheUlamPrimeSpiral/

January 2015 Update - The prime spiral implemented as a Silverlight 5 application.

Silverlight App Removed

It would be nice to see the prime spiral coloured by density, which is something I did back in 1992 with a C program running under DOS 5.0. Here are some photographs (not screen shots) of some my old primitive spirals. Click to popup enlargements.

It's important to reflect and realise what a technologial marvel it is to be able to generate the prime spiral with such ease. In 1992 it took hours of work to write the C code to generate the coloured spirals and I had to manually change and recompile the code each time I wanted to adjust the parameters. It took 10 minutes to write the Mathematica code to generate the spiral, and the resulting high-quality image can be resized, copied and saved. There was a time when it was even more difficult to create such a spiral, read on if you're interested in computer history...

I first had the idea of creating a prime spiral back in the late 1980s when I was working on Fujitsu (Facom) mainframe computers as a systems programmer. Using several hundreds of lines of assembler code (to generate and format the data) and Easytrieve Plus (for the printing) I generated a mock density plot using overprinted character combinations which were printed on 5 strips of 15x11 fan-fold paper which were then trimmed and taped together. I was so impressed with the results that I kept a couple of the spirals rolled-up for years in the garage. After 15 years, I pulled out one of the crumpled plots, flatted the paper and scanned parts of it. It's a shame that the small scans can't reveal the full shape of the artwork.

June 2008 Update -- Thanks to the Canon EOS 400D I can take a photo of the full original 1988 vintage spiral plot. The paper was rather crumpled and the light was poor, so the resulting image isn't that great.

Click to see an enlargement of a section of the mainframe generated prime spiral.		A photo of the full original spiral.

Run a web search for the words "prime spiral" and you will discover that this subject is surprisingly popular and there are many web pages devoted to number spirals of various types.

This web site used to contain a page titled Mathematica Images, but in January 2015 it was migrated over to become this Prime Spirals page. The old "maths art" images I created over 15 years ago had nowhere to go, so I simply pasted them here at the bottom of the spirals page so they won't get lost.

Moiré Pattern

Mixing elementary functions to generate greyscale pixels. A couple of years ago I generated dozens of lovely images using this technique of mixing functions in unusual ways, but I didn't keep the code. One day I'll try to return to this fun topic. In the meantime, here is a trivial surviving example:

rantab = Table[Sin[.01x - .03y x + .02x - .04y], {x, -150, 150}, {y, -150, 150}];
Show[Graphics[Raster[rantab]], AspectRatio -> Automatic]

Wallpaper

Vintage wallpaper images from the mid 1990s (before flat screens broke us out of the traditional 4x3 aspect ratio).