Around 1970-71 when I was in early high school mathematics classes we were learning about famous constants like π, e, the Golden ratio , etc. I said to my friend sitting next to me "I've invented my own constant, which is called Keogh's Constant, and it is defined this way..." and I scribbled down:

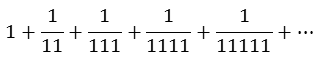
I suspected that the constant had no theoretical or practical use whatsoever, but it was easy to write and it looked curious. Later in the day I thought I had made a mistake and defined something that could be rearranged into a simple sum using high school student knowledge, but I failed to do so and wasn't even sure what sort of a series it was.

In the late 1990s I remembered this series and I fed it into Mathematica V4 to see if it converged to anything recognisable, but I couldn't coax it to produce anything useful. I suspect that V4 did not (yet) have the built-in transformation rules necessary to give me a neat closed form answer (assuming there was one).

In 2012, once again I remembered my old childhood series and I fed it into Mathematica V7 and out popped my answer. Here's what happens:

You can see that Mathematica V7 was able to transform my constant into an expression involving QPolyGamma (The Polygamma function), as well as giving me as many digits as I desired of course. The only slight imperfection in the result is that QPolyGamma arrives in the 3-argument form where the first argument zero is the default and can be omitted. Over previous years I vaguely suspected that my constant would be expressible using the Polygamma function or one of its cousins as I had seen increasingly complex samples in the Mathematica documention where strange power sums were transformed into mixtures of elementary functions and Polygamma.

Just like my school days mystery with Bradley's Integral, Mathematica effortlessly produces a solution decades into the future regarding my "constant". So although my constant is of no practical value, it has accidentally demonstrated amazing progress within the transformation rules built into Mathematica.

15-Dec-2012