NOTE: This page was mostly rewritten in September 2009 to use clearer code samples and plots with Mathematica 6.

In 1975, rumours were passing around Monash University that was an integer, causing a bit of head scratching about this strange "coincidence". At the time we had no calculators or software capable of giving the exact value with suitable precision to verify the claim. Up in the maths labs they had some huge desk calculators that had about 16 digits (I can't remember how many digits exactly), but they weren't accurate enough either. Even now in 2002 my brand new Sharp EL-5120 calculatoronly gives the value as: 2.625374125e17. Mathematica shows us the answer is not an integer, but it's amazingly close.


It turns out the rumour of the value being an integer was sparked by an April Fools joke from Martin Gardner writing in Scientific American. For more information see:

If you can wade through some of the mathematics in the links you will find that the 163 coincidence is tangled up in Heegner Numbers , Class Numbers, Imaginary Quadratic Fields , the j-function and the work of the famous mathematician Ramanujan. The last link is to a book titled Pi Unleashed. This fabulous book discusses the 4000 year history of Pi, covering every imaginable aspect of the number at various levels of difficulty.

Many people have scanned up through higher powers looking for more near-integers coincidences, so one morning in 1997 when I woke up early and couldn't think of anything useful to do, I decided to have a go myself. It's all in good fun, and it's good practice in remembering how to write Mathematica scripts (a few months away from Mathematica and it all looks like gibberish again).

My original 1997 vintage code for Mathematica version 2 was rather crude and now looks embarassing in the age of functional programming, so I've scrapped the original code and replaced it with new code written in Mathematica version 6. The following code generates a full 10000 element list of every E-Root-Pi value, then prints a table of values that are very close to integers, and then plots a larger number of values that are quite close to integers.

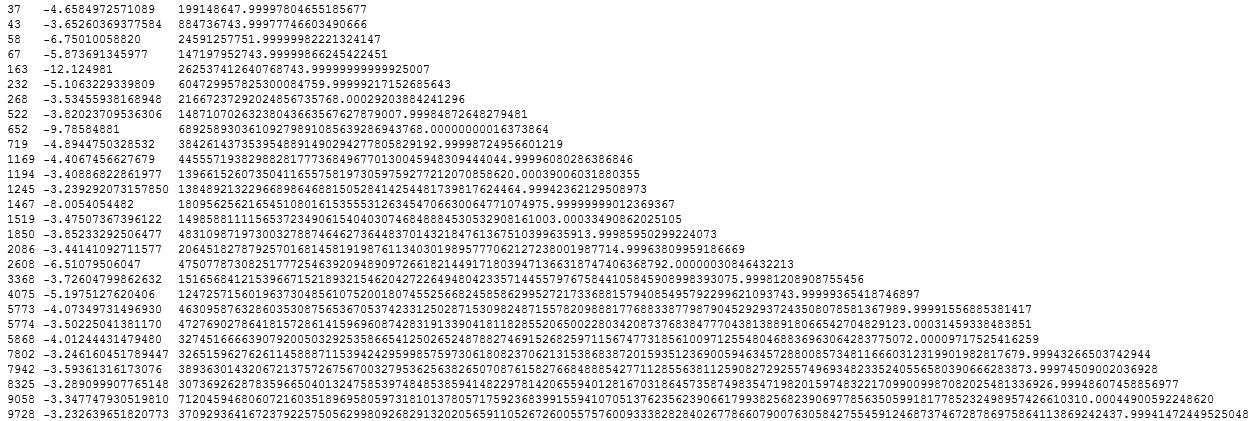
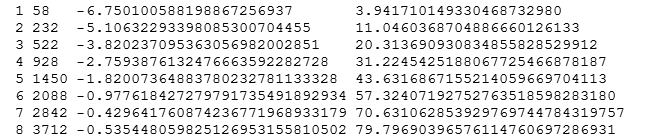
The second column is the base 10 log of the distance the value is from the neatest integer. In September 2009, Stan Owocki emailed me to say that went though a similar E-Root-Pi calculation experiment back in 1990, and he attached an image that plotted the second column of data I've generated above. I was so impressed by Stan's plot that I've reproduced it below almost exactly as his original looked. See Stan's Bartol Research Institute → Home Page.

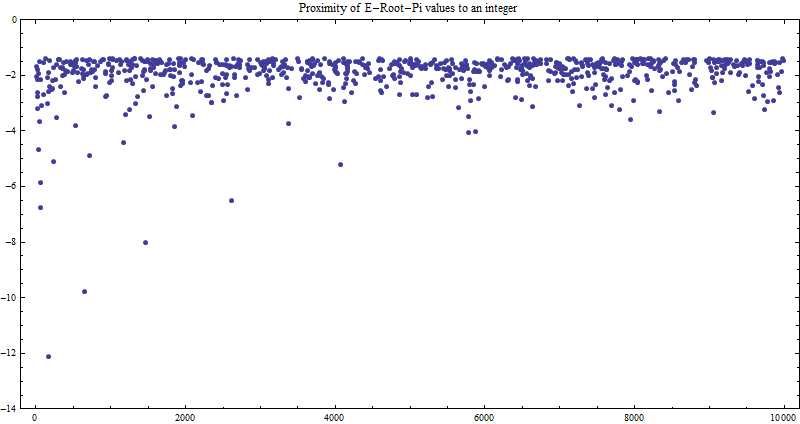
The lower plot points are closer to an integer, so you can see how the logarithm of the distance expands the points and creates an elegant visualisation. The lower left point is the 163 value which is about 10^-12 from an integer (see the left scale). Notice the pattern of points that arch upwards from the 163 value.

Zip of a Mathematica V6 notebook with the above code.

Stan makes the following additonal sharp observations about the plot.

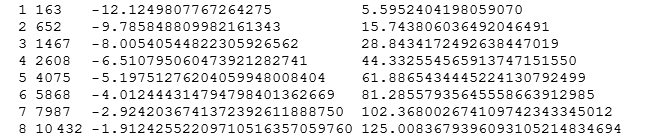
Your comment on my plot calls attention to the beautiful pattern of declining log(error). But doesn't mention what I consider to be one of the most amazing aspects of this, namely each new "echo" represents the case of the original exponent raised to an integer power m=2,3,4 etc. (or multiplying the original n=163 by the square of that power).

Below I attach PDF of code and table for initial n=163. The last column gives the log of first term of binomial expansion of integer and correction. Comparison with the 3rd colulmn of the next row, giving the log of the non-integer part, shows that the integer and correction must again "conspire" to many decimal places (>15 for m=2, the difference between 5.59 and -9.78) to make the new value again so near to an integer. This, and the further continuation for higher powers m really deepens the mystery for me...

Eventually, the cancellation does fade as you get to m=8. For other initial near-integer cases like n=58, which starts out with log(error)=-6.7, the fading destroys the cancellation sooner, but there is still a noticeable spectral series up to m=4 or 5 or so, as shown in the second table below.

Back to: Mathematica